A mí me gustó mucho la película Pi, aunque desde luego es rarita....
Recuerdo que hace unos años se publicaba, no sé si aún lo hace, una revista matemática dedicada únicamente a la sucesión de Fibonacci, cada número con nuevas propiedades.
Una propiedad curiosa de los números es la llamada "conjetura de Goldbach": Todo número par mayor que 2 puede escribirse como suma de dos números primos. Por ejemplo 16=5+11 ¿es cierto? Pues no se sabe. Se cumple para todos los números que han podido calcularse con ordenador, pero nadie ha conseguido aún una demostración, y sigue siendo un problema sin solución...
Saludos,
Rafa
La mágia de los números
Mensajepor acafar » 21 Mar 2008, 22:38
Ah, aunque desvariando un poco, he recordado otra función recursiva interesante, aparte de la de Fibonacci, la de Ackermann:
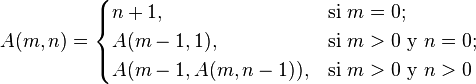
Por ejemplo A(1,1)=A(0,A(1,0))=A(0,A(0,1)) = A(0,2)=3
Lo curioso es lo rápido que crece esta función. Si alguien quiere entretenerse que trate de calcular A(5,2) el número de dígitos de este valor, aunque escribáis muy chiquitín y apretadito, ¡no cabe en el universo conocido! Además la función es convergente, es decir que el valor A(n,m) siempre puede calcularse para todo valor n,m. Sólo hace falta infinita paciencia...
Saludos,
Rafa
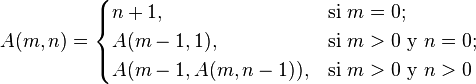
Por ejemplo A(1,1)=A(0,A(1,0))=A(0,A(0,1)) = A(0,2)=3
Lo curioso es lo rápido que crece esta función. Si alguien quiere entretenerse que trate de calcular A(5,2) el número de dígitos de este valor, aunque escribáis muy chiquitín y apretadito, ¡no cabe en el universo conocido! Además la función es convergente, es decir que el valor A(n,m) siempre puede calcularse para todo valor n,m. Sólo hace falta infinita paciencia...
Saludos,
Rafa
Mensajepor Alex » 22 Mar 2008, 18:52
La verdad es que es bastante engorrosa la dichosa ecuación. También como curiosidad, me vienen a la cabeza los "números perfectos" que son aquellos iguales a la suma de sus divisores; ejemplo: 6 =3+2+1; o el 28=14+7+4+2+1 . Pues buscando números perfectos, me encuentro con este que me da el Derive, cuando le solicito que me de el 12º numero perfecto: (Nota: no lo he comprobado)
14474011154664524427946373126085988481573677491474835889066354349131199152128
Supongo que si le pido el 50º se queda sin números!! Ahora te das cuenta de lo inmenso que tiene que ser el infinito1
Ahora te das cuenta de lo inmenso que tiene que ser el infinito1 
En cuanto a la conjetura de Goldbach, sin demostrar, contrasta con la demostración de Lagrange, de algo que yo considero mas difícil todavía:
Todo numero natural es la suma de CUATRO CUADRADOS!!
14474011154664524427946373126085988481573677491474835889066354349131199152128
Supongo que si le pido el 50º se queda sin números!!
 Ahora te das cuenta de lo inmenso que tiene que ser el infinito1
Ahora te das cuenta de lo inmenso que tiene que ser el infinito1 
En cuanto a la conjetura de Goldbach, sin demostrar, contrasta con la demostración de Lagrange, de algo que yo considero mas difícil todavía:
Todo numero natural es la suma de CUATRO CUADRADOS!!
Sol y luna y cielo proclaman al divino autor del mundo...
-
Guest
Mensajepor Guest » 22 Mar 2008, 20:02
Estoy leyendo todas estas curiosas series y enmudezco. Pero tu última propuesta Alex, no sé si va en broma. 
De referirse a la suma de cuatro números, resulta una perogrullada. Ya sabemos que cualquier cantidad es la suma de cuatro cuartos de tal cantidad.
O ¿a qué se refiere?. Me temo que no entendí.
Cualquier cuadrado de valor entero positivo, se puede dividir en cuatro cuadrados idénticos, por lo que la suma de ellos es el total. Y serán cuatro cuadrados de lado mitad del total.
Como me temo que no es esto lo que propone tu anunciado, disculpa mi corta mira. Y posiblemente todo el mundo lo entienda como debe corresponder.
Saludos del Abuelo.

De referirse a la suma de cuatro números, resulta una perogrullada. Ya sabemos que cualquier cantidad es la suma de cuatro cuartos de tal cantidad.
O ¿a qué se refiere?. Me temo que no entendí.

Cualquier cuadrado de valor entero positivo, se puede dividir en cuatro cuadrados idénticos, por lo que la suma de ellos es el total. Y serán cuatro cuadrados de lado mitad del total.
Como me temo que no es esto lo que propone tu anunciado, disculpa mi corta mira. Y posiblemente todo el mundo lo entienda como debe corresponder.

Saludos del Abuelo.

Mensajepor franc » 22 Mar 2008, 22:25
HAL9000, ya la he descargado y la veré ésta noche, aunque la que he descargado se llama Pi, la Teoría del Caos.
Los números no es que sean mágicos, son símbolos y medidas, inventados por nosotros para vislumbrar de una forma más comprensible la naturaleza, la magia está cuando nos reafirman en la experiencia los valores dados a aquella.
Acafar escribió:
Una propiedad curiosa de los números es la llamada "conjetura de Goldbach": Todo número par mayor que 2 puede escribirse como suma de dos números primos. Por ejemplo 16=5+11 ¿es cierto? Pues no se sabe. Se cumple para todos los números que han podido calcularse con ordenador, pero nadie ha conseguido aún una demostración, y sigue siendo un problema sin solución...
Siempre que se cumpla esto es cierto:
1+6 = 7 5+1+1 =7


saludos
Los números no es que sean mágicos, son símbolos y medidas, inventados por nosotros para vislumbrar de una forma más comprensible la naturaleza, la magia está cuando nos reafirman en la experiencia los valores dados a aquella.
Acafar escribió:
Una propiedad curiosa de los números es la llamada "conjetura de Goldbach": Todo número par mayor que 2 puede escribirse como suma de dos números primos. Por ejemplo 16=5+11 ¿es cierto? Pues no se sabe. Se cumple para todos los números que han podido calcularse con ordenador, pero nadie ha conseguido aún una demostración, y sigue siendo un problema sin solución...
Siempre que se cumpla esto es cierto:
1+6 = 7 5+1+1 =7



saludos
Ubi dubium ibi libertas:
Donde hay duda, hay libertad.
Preserva tu derecho a pensar,
puesto que incluso pensar erróneamente,
es mejor que no hacerlo en absoluto.

HIPATIA
http://elclariscuro.blogspot.com/
Donde hay duda, hay libertad.
Preserva tu derecho a pensar,
puesto que incluso pensar erróneamente,
es mejor que no hacerlo en absoluto.

HIPATIA
http://elclariscuro.blogspot.com/
- inavarro88
- Mensajes: 1043
- Registrado: 21 Ene 2005, 00:00
- Ubicación: Tenerife, Islas canarias
- Contactar:
Mensajepor inavarro88 » 22 Mar 2008, 22:54
franc escribió:Los números no es que sean mágicos, son símbolos y medidas, inventados por nosotros para vislumbrar de una forma más comprensible la naturaleza, la magia está cuando nos reafirman en la experiencia los valores dados a aquella.
Creo que la matemática es ya un arte por si solo. No tienen necesidad de unirse al mundo físico para ser maravillosas. Eso sí, cuando se unen a la física...

<a href="modules.php?name=Equipo&op=ver_equipo&usuario=inavarro88"> Tengo telescopio en mi perfil.</a> Oh, Be A Fine Girl, Kiss Me!!
Mensajepor acafar » 22 Mar 2008, 22:56
Disiento franc (es más divertido así  ). Nosotros no hemos inventado los números, estaban ahí . No hubiéramos sido capaz de inventar algo tan lleno de misterio, de sorpresas, de belleza, de armonía, que nos sigue maravillando a cada paso. Los números son un reflejo del universo, no una pesa ni una medida que si son inventos humanos.
). Nosotros no hemos inventado los números, estaban ahí . No hubiéramos sido capaz de inventar algo tan lleno de misterio, de sorpresas, de belleza, de armonía, que nos sigue maravillando a cada paso. Los números son un reflejo del universo, no una pesa ni una medida que si son inventos humanos.
Saludos,
Rafa
 ). Nosotros no hemos inventado los números, estaban ahí . No hubiéramos sido capaz de inventar algo tan lleno de misterio, de sorpresas, de belleza, de armonía, que nos sigue maravillando a cada paso. Los números son un reflejo del universo, no una pesa ni una medida que si son inventos humanos.
). Nosotros no hemos inventado los números, estaban ahí . No hubiéramos sido capaz de inventar algo tan lleno de misterio, de sorpresas, de belleza, de armonía, que nos sigue maravillando a cada paso. Los números son un reflejo del universo, no una pesa ni una medida que si son inventos humanos.
Saludos,
Rafa
Mensajepor acafar » 22 Mar 2008, 23:05
Por cierto Carlos, el resultado de los cuatro cuadrados que dice Alex no es de broma y tiene su miga (la demostración, al menos). Aparece por primera vez en la aritmética de Diofanto, aunque la demostración se debe a Lagrange (siglo XIX).
Por ejemplo:
6 = 2^2 + 1^2 + 1^2 + 0^2 = 4+1+1+0
15 = 3^2 + 2^2 +1^2 + 1^2 = 9+4+1+1
Por supuesto muchos números se pueden poner como suma de menos cuadrados, el propio 6 es evidentemente la suma de 3 cuadrados, pero para algunos como el 15 no es posible hacerlo con menos de 4.
Saludos,
Rafa
Por ejemplo:
6 = 2^2 + 1^2 + 1^2 + 0^2 = 4+1+1+0
15 = 3^2 + 2^2 +1^2 + 1^2 = 9+4+1+1
Por supuesto muchos números se pueden poner como suma de menos cuadrados, el propio 6 es evidentemente la suma de 3 cuadrados, pero para algunos como el 15 no es posible hacerlo con menos de 4.
Saludos,
Rafa
Mensajepor Alex » 22 Mar 2008, 23:22
De referirse a la suma de cuatro números, resulta una perogrullada. Ya sabemos que cualquier cantidad es la suma de cuatro cuartos de tal cantidad.
O ¿a qué se refiere?. Me temo que no entendí. Embarassed
Carlos, estamos hablando de numero naturales:
n = a^2+b^2+c^2+d^2; n,a,b,c,d pertenecen a N={0,1,2,...}
(esto quiere decir que no interviene ningún numero racional a/b ni por supuesto ningún irracional como raices de numeros que no son cuadrados perfectos)
Carlos
Cualquier cuadrado de valor entero positivo, se puede dividir en cuatro cuadrados idénticos
Esto no es cierto. Por ejemplo 15^2 = 225 y 225 no es divisible por 4, ni 15 es divisible por 2, esto sería factible en el conjunto de los numeros Reales.
De todas formas, lo jodido es demostrarlo, igual que la propuesta de Goldbach, que aludia acafar
Sol y luna y cielo proclaman al divino autor del mundo...
Mensajepor franc » 22 Mar 2008, 23:35
Alex dijo:
Esto no es cierto. Por ejemplo 15^2 = 225 y 225 no es divisible por 4, ni 15 es divisible por 2, esto sería factible en el conjunto de los numeros Reales.
De todas formas, lo jodido es demostrarlo, igual que la propuesta de Goldbach, que aludia acafar
Siempre que se cumpla esto es cierto:
225/4 = 56.25 5+6+2+5 = 18
1+8 = 9
2+2+5 = 9
1+5 = 6 6/2 = 3
7.5 su digital 7+5 = 12 su digital 1+2 =3


saludos
Esto no es cierto. Por ejemplo 15^2 = 225 y 225 no es divisible por 4, ni 15 es divisible por 2, esto sería factible en el conjunto de los numeros Reales.
De todas formas, lo jodido es demostrarlo, igual que la propuesta de Goldbach, que aludia acafar
Siempre que se cumpla esto es cierto:
225/4 = 56.25 5+6+2+5 = 18
1+8 = 9
2+2+5 = 9
1+5 = 6 6/2 = 3
7.5 su digital 7+5 = 12 su digital 1+2 =3


saludos
Ubi dubium ibi libertas:
Donde hay duda, hay libertad.
Preserva tu derecho a pensar,
puesto que incluso pensar erróneamente,
es mejor que no hacerlo en absoluto.

HIPATIA
http://elclariscuro.blogspot.com/
Donde hay duda, hay libertad.
Preserva tu derecho a pensar,
puesto que incluso pensar erróneamente,
es mejor que no hacerlo en absoluto.

HIPATIA
http://elclariscuro.blogspot.com/
Volver a “Ciencias en General”
Ir a
- FUNDAMENTOS DE ASTRONOMÍA
- Principiantes
- Astronaútica y Misiones Espaciales
- Sol, Luna y Planetas
- Cuerpos Menores (Cometas, Asteroides y Meteoros)
- Astronomía extrasolar (Galaxias, Nebulosas, Cúmulos,...)
- Historia de la Astronomía
- ASTRONOMÍA TEÓRICA Y COSMOLOGÍA
- Física Clásica o Newtoniana
- Física Cuántica y Relatividad
- Cosmología y Universo
- ASTRONOMÍA PRÁCTICA Y OBSERVACIÓN
- Telescopios e Instrumentos Ópticos
- Prismáticos
- Monturas y Accesorios no Ópticos
- Astrobricolaje
- Técnicas de Astrofotografía
- Escaparate Astrofotográfico
- Estrellas dobles
- Observación
- Eventos y efemérides
- Astronomía CCD
- Cielo oscuro
- Lugares de observación
- RECURSOS ASTRONÓMICOS
- Didáctica de la Astronomía
- Software e internet
- Astronomia y Medios de Comunicación
- OTRAS CIENCIAS & ARTES AFINES
- Ciencias en General
- Películas y Libros
- EVENTOS, ACTIVIDADES Y ASOCIACIONISMO
- Tablón de Anuncios y Salidas
- Andalucía, Ceuta y Melilla
- Aragón
- Cantabria
- Castilla y León
- Castilla-La Mancha
- Cataluña
- Comunidad de Madrid
- Comunidad Valenciana
- Extremadura
- Galicia
- Islas Baleares
- Islas Canarias
- La Rioja
- Navarra
- País Vasco
- Principado de Asturias
- Región de Murcia
- Ediciones Históricas de ASTROMARTOS
- AstroMartos 2015
- AstroMartos 2014
- AstroMartos 2013
- AstroMartos 2011 - DÉCIMO ANIVERSARIO
- AstroMartos 2010
- AstroMartos 2009
- AstroMartos 2008
- AstroMartos 2007
- AstroMartos 2006
- AstroMartos 2005
- AstroMartos 2004
- Foro de e-socios
- MERCADILLO
- Material de Observación
- Compra
- Venta
- Intercambio
- Otro tipo de material
- PÁGINA WEB
- Preguntas, Respuestas, Sugerencias, ....
Identificarse
Suscríbete como E-SOCIO/A
DONACIONES

IN MEMORIAM
El legado de Arbacia
13.791 mensajes de nuestro usuario más activo. Te invitamos a descubrir la base documental y de ayuda que nos dejó en este ENLACE

(Foto: Wikipedia)
¿ Quién fue nuestro usuario Arbacia ?
Patricio Domínguez Alonso fue un paleontólogo español, gran amante de la Astronomía y Divulgador Científico.
Doctor en Ciencias Biológicas (1999) y especialista en Biología Evolutiva fue profesor de Paleontología en la Facultad de Ciencias Geológicas de la UCM. Miembro del Instituto de Geociencias (CSIC-UCM) desde su creación, estaba integrado en la línea de Investigación del Centro “Episodios críticos en la historia de la Tierra”.
Su trabajo de investigación se centró en el origen de los vertebrados, evolución temprana de aves y estudios sobre el cuaternario en el Caúcaso. Para ello desarrolló estancias de investigación en Reino Unido, Estados Unidos, Brasil, Armenia, China y Honduras (Fte. Wikipedia)
Como aficionado a la Astronomía, desde 2008 fue Presidente de la Asociación Astronómica AstroHenares y socio destacado de la Asociación Astronómica Hubble. Desde 2005 y durante 8 años fue moderador activo y permanente de este foro, convirtiéndose en el usuario más prolífico del mismo y en uno de los garantes de su buen funcionamiento.
Con el apoyo de la Asociación Hubble y la difusión del foro, organizó algunas de las reuniones de aficionados a la Astronomía más importantes de España, como la de Navas de Estena en los Montes de Toledo, conocida como “AstroArbacia”.
Podemos afirmar sin temor a equivocarnos que su pérdida inició el declive del foro allá por 2013. Por eso, tras su renovación queremos rendir homenaje desde la Asociación Hubble a su figura como aficionado a la Astronomía, como persona y como gran amigo de los administradores, moderadores y muchos de los usuarios del foro, a los que siempre ayudaba con agrado y sabiduría en multitud de temas.
Nos vemos en las estrellas, amigo

¿ Quién fue nuestro usuario Arbacia ?
Patricio Domínguez Alonso fue un paleontólogo español, gran amante de la Astronomía y Divulgador Científico.
Doctor en Ciencias Biológicas (1999) y especialista en Biología Evolutiva fue profesor de Paleontología en la Facultad de Ciencias Geológicas de la UCM. Miembro del Instituto de Geociencias (CSIC-UCM) desde su creación, estaba integrado en la línea de Investigación del Centro “Episodios críticos en la historia de la Tierra”.
Su trabajo de investigación se centró en el origen de los vertebrados, evolución temprana de aves y estudios sobre el cuaternario en el Caúcaso. Para ello desarrolló estancias de investigación en Reino Unido, Estados Unidos, Brasil, Armenia, China y Honduras (Fte. Wikipedia)
Como aficionado a la Astronomía, desde 2008 fue Presidente de la Asociación Astronómica AstroHenares y socio destacado de la Asociación Astronómica Hubble. Desde 2005 y durante 8 años fue moderador activo y permanente de este foro, convirtiéndose en el usuario más prolífico del mismo y en uno de los garantes de su buen funcionamiento.
Con el apoyo de la Asociación Hubble y la difusión del foro, organizó algunas de las reuniones de aficionados a la Astronomía más importantes de España, como la de Navas de Estena en los Montes de Toledo, conocida como “AstroArbacia”.
Podemos afirmar sin temor a equivocarnos que su pérdida inició el declive del foro allá por 2013. Por eso, tras su renovación queremos rendir homenaje desde la Asociación Hubble a su figura como aficionado a la Astronomía, como persona y como gran amigo de los administradores, moderadores y muchos de los usuarios del foro, a los que siempre ayudaba con agrado y sabiduría en multitud de temas.
Nos vemos en las estrellas, amigo
Bienvenidos al nuevo Foro HUBBLE
Hemos tardado un poco... pero ya estamos on-line con una nueva imagen, software actualizado y base de datos optimizada
Desde Hubble os damos las gracias por vuestra paciencia y os deseamos que lo disfruteis.
Desde Hubble os damos las gracias por vuestra paciencia y os deseamos que lo disfruteis.
- Todos los horarios son UTC+01:00
- Arriba
- Borrar todas las cookies del Sitio
Asociación Astronómica HUBBLE | Martos (Jaén)
Foro de Astronomía y Astrofotografía. Desde 2004 en Internet
Todos los Derechos Reservados
Enlaces
Powered by phpBB ® | © 2017 Asociación Astronómica HUBBLE



